Comments about the CRU hack...

http://www.realclimate.org/index.php/archives/2009/11/the-cru-hack/

http://www.realclimate.org/index.php/archives/2009/11/the-cru-hack-context/

Sane Value Decomposition

Oh no! Another article about SVD! Well, this one is not specifically about SVD, but it is describing some of my theories about parametrization of SVD and why so many people get different results and possibly why I didn't win! :).

To explain my theories, we need to first understand SVD in some reasonable way. The SVD formula goes:

A = U Ʃ V

Which means that the above (for the purposes of this explanation) square matrix is decomposed into other equally sized matrices U, Ʃ and V. The U and V are orthogonal matrices, the Ʃ matrix contains the so-called singular values.

More intuitively said, the U matrix is a depiction of the actions of the rows in the matrix, whereas the U matrix is a depiction of the columns. Multiplying the values in a row of U with a column in the V transposed matrix (V.T), multiplied by the value in the diagonal of Ʃ that corresponds to the row,column selected, you get the value of the original cell in A. So, svd on a matrix A gives a strict representation of the values in A, but in a different 'decomposed' way.

But we don't have to go all fully-dimensional, because having all matrices around means we need three times more storage than the original one, and that's not the point. So the idea is to reduce the dimensions of each matrix and keep only the first x around. x however should be a reasonable percentage of the rank (row/column size), because if x is too low relatively speaking, you're not getting good results. I will show how this all works in more detail using python, a language that's very quickly starting to become my favourite language for experiments!

Example:

This is a square matrix with random values between 1-5 of n x m = 5 x 5 dimensions. So 25 numbers in total.

[ [3,5,2,4,4],
  [3,2,5,5,3],
  [4,4,5,4,3],
  [2,3,4,5,2],
  [1,5,5,2,2] ]

One thing I discovered (which many sites probably mention in not so readable terms :), is that when the matrix becomes relatively large, the first singular value on the diagonal approximates the average multiplied by the square root of the total numbers available in the matrix ( in the case above, the average is 3.48 ).

Ʃ(1) = avg * sqrt( number_of_cells )

The second singular value for larger, irregular matrices is approximated by:

Ʃ(2) = sqrt( 2 * Ʃ(1) )

So there certainly is a pattern being generated. Each singular value in the decomposition is actually a gain factor. So, if the matrix is really, really large, the singular values become in the orders of 1000's and the values in the first columns of U, V become 1/1000 in the case of this particular range for the Netflix data ( 1-5 across the matrix ).

Here are the actual singular values when the matrix is decomposed:

sigma = mat( [ 17.76224954, 3.5139895, 3.16968094, 1.60407331, 0.73105457 ] )

And here are U and V:

mw = mat( [[-0.44379232, -0.33273609 ,-0.80072792 , 0.11314317 ,-0.19587877], \
    [-0.4616133  , 0.58960592 , 0.15588499 ,-0.08007446 ,-0.63919166], \
    [-0.5053614  , 0.05135939 , 0.03629005 ,-0.69454331 , 0.50819749], \
    [-0.41956887 , 0.28391073 , 0.09075436 , 0.69668699 , 0.49974748], \
    [-0.39816248 ,-0.67705869 , 0.57007135 , 0.11412068 ,-0.21225762] ] )

cw = mat( [[-0.33638547 , 0.24667399 ,-0.32741104 ,-0.73031105 , 0.43063272], \
    [-0.47365356 ,-0.80039862 ,-0.13379567 , 0.1795791  , 0.29131499], \
    [-0.52873629 , 0.082443   , 0.81168849 ,-0.18044758 ,-0.14913599], \
    [-0.50662787 , 0.5372694  ,-0.21592459 , 0.61450025 , 0.17445861], \
    [-0.3553354  ,-0.05530591, -0.4116298  ,-0.15564457 ,-0.82280841] ] )

Notice how in the U and V matrix, the numbers are maintained at roughly the same magnitude throughout each dimension (you need to read rows and each column further to the right is one dimension deeper). This can be done because if you follow the implementation of SVD correctly, the singular value is the gain factor. So, choosing the correct 'gain' is essential for proper functioning of the model, or you need to adjust the parameters in each dimension.

What some people did in Netflix for example is to assume a gain of 1.0f (the singular values were not used) and then initialize each dimension to some 'low' value. Naturally, you can see that these 'low' values are actually really low in the beginning, but once the model starts to hit other dimensions, you may suddenly hit a gain factor that is above the singular value of the actual matrix Ʃ. That means the model becomes immediately instable and will start producing very high values.

Let's look at a regular matrix:

[[4 4 4 4 4]
 [5 5 5 5 5]
 [3 3 3 3 3]
 [2 2 2 2 2]
 [1 1 1 1 1]]

U:
[[-0.54446573 -0.21442291  0.76382282 -0.25982498  0.08152026]
 [-0.65208362 -0.46955287 -0.55122106  0.17692309  0.13842191]
 [-0.3619848   0.49755586  0.15572615  0.71006801 -0.30489008]
 [-0.31846257  0.36154464 -0.26944015 -0.60360543 -0.57526478]
 [-0.21422565  0.59604242 -0.12602146 -0.1807017   0.74182633]]
sigma:
[ 17.71717246   1.04811144   0.           0.           0.        ]
VT:
[[-0.53913501  0.50275905  0.61561055 -0.13109677  0.24577241]
 [-0.40915723 -0.26153467  0.04808419  0.872681   -0.01748586]
 [-0.35699995 -0.56822929 -0.1744093  -0.31507809  0.64805378]
 [-0.37793419 -0.44513203  0.23939904 -0.33777929 -0.69829541]
 [-0.52119151  0.39724791 -0.72868447 -0.08872685 -0.17804491]]

Whoops, what happened? We now only have 2 dimensions left, but after the third dimension all values are 0? This is because the matrix is so regular that it can be described perfectly with two factors. Hmmm.... So if there is good regularity in the data, then we need less numbers to represent the matrix! Of course, the above is taken to the extreme, but looking at recommendation systems, there are certainly regularities:

• Some users are very constant in their ratings and generally use a scale of 4-5 for everything.
  
• Nobody wants to rent bad items, those are generally avoided, so the likelihood that someone gets an unexpectedly bad item is relatively low. That means that relatively speaking, ones and twos occur less often than 3-5.

In essence also, you don't get a lot of information if rows or columns only contains 5's. The information is in the irregularities actually (or temporal trends, but that's another story! :).

More on the theory... Suppose we stick with the irregular 5x5 matrix above. It's basically random. I wanted to find out how fast I can converge to this 5x5 matrix using both some clever initialization techniques and gradient descent. (gradient descent is where you assume some random factors mw/cw, then calculate using those factors your prediction, compare this with the real number and adjust the factor by the error that you get from the comparison. This way, you can "train" the decomposed matrices U and V individually without having to store the entire matrix A in memory (which you don't have anyway, except for a small percentage of, say, 1% of it ).

When you look at the matrix, in the first feature / component that you calculate, you need to make a jump from 0 to somewhere in the 1-5 region. And all numbers 1-5 are positive. This is good, because you know that either the features need to be both positive or both negative. Make your choice. A good approximation for each feature further on is the sqrt( average ) of each respective column and row. This is because in the final calculation, the value in the cell is hopefully already quite well approximated by:

Aij = Ri1 * Cj1 * Ʃ1

In practice, for slightly larger matrices and those that are totally random, the root mean square error of each estimation vs. the real value will be around 1.41 or so. Of course, this is a function of the range used in the actual matrix A. It also shows that if the matrix is highly irregular, you're not converging very quickly to an error rate where your model becomes useful for making nice approximations.

Learning matrices is a tricky operation. Assuming the matrix from above, which has full information available, is square and relatively easy to learn, if the learning rate is too high, the model becomes unstable and the RMSE increases at some point exponentially. Ideally, you start from a good initial point, so that the gradient descent only needs to settle to the minimum, but this is only possible in the start situation. A good initialization of a model uses the following formulas:

1. Calculate GLOB_AVG from entire matrix
   
2. Ʃ1 = GLOB_AVG * sqrt( num_cells )
   
3. Ri1 = sqrt( Ravg / Ʃ1 )
4. Cj1 = sqrt( Cavg / Ʃ1 )
5. lrate_first_cycle == slow (it's almost there) == 1 / Ʃ1
6. INIT = ( GLOB_AVG / ( 2 * sqrt( 2 * GLOB_AVG * sqrt( num_cells ) ) ) )
   
7. Rix (x>1) = rand( -INIT, INIT )
8. Cjx (x>1) = rand( -INIT, INIT )
9. lrate_other_cycles == depends on the data :)
   

The latter comment was made, because I don't have sufficient empirical insight yet into how the learning rate should be calculated. It also depends on the objective. If you have full data available and you just want to deconstruct quickly, then you might want to go for fast and high learning rates. But for others, accuracy is more important and not having too many factors lying around. Then a fast enough, but much slower learning rate is more appropriate.

I'm still looking into data inside matrices that may be imbalanced. E.g., having 17000 ratings on a single row vs. sometimes 1-5 ratings in a column. The problem here is that a single row is updated 17000 times vs. an update frequency of 5 for a column. Obviously, this might give rise to a very quick imbalance in the model and maybe trying out different learning rates, one for columns and one for rows may be an answer. Some practical experiments there however have shown that this further destabilizes the model... so what can you do?? :).

Netflix prize revisited

The netflix prize has been over for some months. I ended up 215th in the high score table. Considering my involvement over time, it's probably where I should have ended up. Other groups have been at the prize for three years and rightfully ended up in the top 40.

If you still have a research interest in the Netflix prize, you can still download the data from the UCI Machine Learning Repository. This set also includes the actual ratings that were used to rate the submissions. It also includes the winning submission set.

A very interesting implementation for solving this problem is the PyFlix implementation. This implementation requires the downloaded data, but converts it into a binary database that is mmap-ed later into the process space. That's quite clever, because using mmap you can also dump some index or mmap some index once you need it. Certainly, you shouldn't do this within loops, but it goes to show that for performance computing, using files is generally a much better approach than databases. Of course you need to work on the files to get them to do something for you.

If you look at the Basic Usage of the Trac page of PyFlix, you'll see some examples of the very nice interface that was built on top of the data. Now, researchers often have not so much data to proof their concepts and the interface built on top of the netflix data in such a way is remarkably elegant for looking into similarities and trying out a couple of concepts from the python interpreter directly.

I have found however that a production implementation of svd or any other algorithm isn't truly viable in Python because of the CPU constraints and the overhead in a number of things. One of those things being the following flags (gcc) for the binaries built on my machine:

-Wall -march=core2 -mtune=core2 -O2

These show that the binaries to be built are tuned specifically to my processor that I am running, instead of generic "i386" architectures. I'm also no expert on Python, so there may be many ways to totally optimize python such that it runs much better. The flags above will generate code that is much more efficient and reduces a single cycle of 27 seconds on generic i386 architectures to 7 secs in total.

Although programmers don't worry about memory in general that much, since they don't need to (readibility of code and other quality attributes need to be paid attention to as well), for certain loops that are executed a very large number of times (in the millions), it becomes much more important to focus on the actual performance of that loop. This is a very nice article about memory, written by the maintainer of the glibc library of Linux. The glibc library is the glue between the kernel and your application basically and it has a number of handy low-level utility functions that every application uses (like strlen, strstr, etc.).

One of the important aspects of maintaining performance is trying to sort data (if possible functionally and technically), such that the processor doesn't get a cache miss to acquire the data. It will then be much quicker in those kinds of loops. Another kind of performance hog is the ordering of data, for example:

my2DArray[ ROWS ][ COLS ];

When cycling through this loop, you'll want to do this by rows first, then cycle on the columns. The columns are probably linearly aligned in memory, one after the other. So you'd typically iterate through this array through:

for i = 0 to ROWS:
  for j = 0 to COLS:
      my2DArray[ i ][ j ]

Compare that to:

for j = 0 to COLS:
  for i = 0 to ROWS:
      my2DArray[ i ][ j ]

The second has cache misses all over the place, which is very bad for performance. Ideally, for computational tasks you find an algorithm that both keeps data close in the processor cache as long as possible, but of course only if that is feasible.

The implementation of pyflix is sneakily reading from disk and doing quite a bit of things in the background for every iteration of the rating loop. This is severely hurting performance in the long run. The good thing is that there's a very elegant API to access the data for other purposes and this API does include a rather fast index. It's as if a very tiny little specific database engine was written to access the data, which is a remarkable and impressive feat by itself!

SVD in Python

Here's a small example of Singular Value Decomposition using Python:

from scipy import linalg, mat, dot;
matrix = mat( [[2,1,0,0], [4,3,0,0]] );
print "Original matrix:"
print matrix
U, s, V = linalg.svd( matrix )
print "U:"
print U
print "sigma:"
print s
print "VT:"
print V
dimensions = 1
rows,cols = matrix.shape
#Dimension reduction, build SIGMA'
for index in xrange(dimensions, rows):
 s[index]=0
print "reduced sigma:"
print s
#Reconstruct MATRIX'
reconstructedMatrix= dot(dot(U,linalg.diagsvd(s,len(matrix),len(V))),V)
#Print transform
print "reconstructed:"
print reconstructedMatrix

This code prints the following:

Original matrix:
[[2 1 0 0]
[4 3 0 0]]
U:
[[-0.40455358 -0.9145143 ]
[-0.9145143   0.40455358]]
sigma:
[ 5.4649857   0.36596619]
VT:
[[-0.81741556 -0.57604844  0.          0.        ]
[-0.57604844  0.81741556  0.          0.        ]
[ 0.          0.          1.          0.        ]
[ 0.          0.          0.          1.        ]]
reduced sigma:
[ 5.4649857  0.       ]
reconstructed:
[[ 1.80720735  1.27357371  0.          0.        ]
[ 4.08528566  2.87897923  0.          0.        ]]

And with one more dimension for sigma:

reduced sigma:
[ 5.4649857   0.36596619]
reconstructed:
[[ 2.  1.  0.  0.]
[ 4.  3.  0.  0.]]

This is how you can use Python for quick tests and experiments on SVD.

Abstract thought

Thought... what is it? I've posted before on the topic of consciousness and thought. Without any final conclusion, the topic of thought is discussed in philosophy with differing opinions on the matter. Some say that thought has mystic properties and is only reproducible in biological matters, some in that camp go as far to state that thought is purely human and is what separates us from animals. Could be, since there surely are specific differences in the way we learn, reason and behave, even compared to monkeys. See "Ape Genius" here for example. The last video talks about a very important difference, namely pointing. The questions posed in the research is whether apes are more or less thinking like us or share specific traits that make them behave like us. Looking at the videos and specifically the parts about cooperation and learning, I have personally come to the conclusion that there is not that much in common (the problem is that in a way, apes look more like us than, say, horses, so we're inclined to believe they think like us for that reason. But are they really the same once you completely ignore the 'look-alike'? ). Back to the question at hand... there are other streams in philosophy that believe thought is computational. Then there are once again subdivisions in that region. Some say that the mind is partly computational, but has other traits that are incredibly hard to model and execute on a computer for example.

Scientists now believe that they can recreate thought by replicating neural networks. So the idea is to think of a common task and then proof that this task can be satisfiably executed by an artificial neural network running in a computer. The problem here is that the neural network is trained for a very particular task and there is no reasoning taking place other than the execution of that particular task. So the neural network expects a range of inputs and will calculate the correct output based on those. If the inputs are out of range, the output is not guaranteed to be useful. Also, you will only get a meaningful output for a specific purpose, not an output that is meaningful in different scenarios.

The biggest problem here is that we can't think in sufficiently abstract terms and the relations between those terms. Because we cannot imagine 'pure thought', what it looks like and how it can be alternatively represented, we keep pushing buttons in the hope that somewhere we find an interesting response somewhere that indicates some kind of causality of the external world and internal processing.

In order to simulate thought in a computer, one must assume that thought is purely computational, otherwise the motivation and the execution of the research is contradictory. Pure computational thought requires us to think differently about representations and find other ways to represent parts of the meta-model of the outside world. The world out there has a form and when we see a cat, we don't pick it up, put it in our head and reproduce it later in thought. So, thought requires us to model those things differently in our minds such that they can be reproduced later. Whether this be a word or a number is not truly relevant. The relevance is related to how the relations between these concepts can be maintained. So, reasoning about things isn't exactly about representing the concepts, but about representing the relations between concepts, what things do to one another or how they are typically related.

Singular Value Decomposition, often discussed on this blog within the context of collaborative filtering, has the ability to express patterns of co-occurrence or relations between numbers or items. And here starts the rub. For SVD to be useful, the designer / modeler needs to determine the correct way to put the numbers into the matrix before the calculation is started. The model dictates for example that users go into columns and movies go into rows. Then for each combination, a number is inserted, yielding a huge matrix of interrelations between instances. The interesting thing here is then that one movie relates to many users and one user relates to many movies. So, in essence, the preference of a user is modeled within this matrix and related to the type and characteristics of a movie. In a sense, this means that preference is modeled against characteristics. We don't have any data available about movie characteristics or user preferences directly, but generating this matrix we can suddenly start reasoning with those, although the exact meaning of preferences and meaning of characteristics, appearing as numbers, may not be derive-able.

And here goes... in order to make those preferences and characteristics meaningful, one should have a classification system at hand that can compare classes with one another. Classification means comparing two things to one another and trying to find the most important characteristic that make them match or differ. That operation is different from the calculation performed earlier.

So this goes back to our incapacity to think in truly abstract terms. We can get a feeling for something, but then if it is abstract, can't describe it. Although we are certain about incompatibility, incongruence or similarity for example. A computer model where these abstracts can be manipulated and translated into something meaningful, classified and everything backwards is going to be a very important step.

I think of the brain not as a huge number of neurons that are interconnected, but I think of each neuronal group as some kind of classifier or work item. In that sense, one can question whether it makes sense to simulate 100 billion neurons if the total effect of those biological computations can be simulated more effectively using stricter and cheaper mathematical operations, or a simulation of neuron groups in a neural group network instead, severely reducing the dimensions that are (thought) to be necessary.

This is a great question for research. Can a machine that is constructed from bits, which are 0's and 1's, therefore have no intermediate state, work with numbers and symbols in such a way that it starts to approximate fluid thought?

Building a mapserver with a karmic koala

I've updated my Linux system to Karmic Koala over the weekend. It seems to work quite well. For the first time, I decided to kill all the binaries that somehow made it to my machine over a course of 2 years and do a fresh binaries install, keeping my home mount with data. That worked out well and the machine even booted my RAID-0 array with dmraid without any problems this time. Ubuntu 9.10 works like a treat, you should try it!


Getting down to business, if you want to find out how Google / TeleAtlas renders maps, here's a page that gives you an idea how the process works. A mapserver is basically an image server with a HUGE, HUGE, HUGE number of tiles behind it. Each zoomlevel maintains its own set of images basically, so that's why adding a zoomlevel to a finer-grained level will be costly space-wise. The tiles are constructed by adding GIS information of different types together from a rather large database. The tutorial that I found here is very easy to follow and the most comprehensive on the subject.

In this tutorial, they end up building a little world map, which I attempted and worked out, as you can see. The world map on the right was constructed by the information of SHAPE files on my server. The overview is a very generic image, but the information in the SHAPE file is so great, that I can zoom in to great extents and produce the complete coastline of Antarctica or any country in Europe. Thanks to the efforts of the Openstreetmaps project that is and people and organizations that collaborate with them. Notice also how the world seems to appear slightly distorted. I think this is related to the chosen projection method.

Well, once that is working, you can load your own spatial data in postgis and postgres and start drawing specific parts of your interest on detailed images. Instead of writing your own programs to do that, just use the utilities and scripts of the mapnik project. An example of that is here, central Amsterdam:

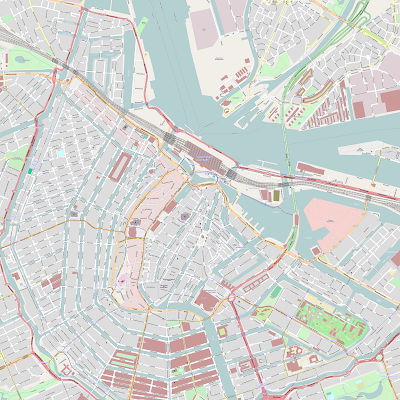So this is great. I can now produce very detailed streetmaps of any region in Holland, reason about those places and ways through a database with spatial reasoning predicates, find out extents of regions, and so forth. Mapnik also provides scripts to generate tiles from a given 'planet' database. Tiling a country however can produce a very large amount of data on your PC, so use with care :). The above image was produced using standard styling rules. It is possible to adjust this styling or replace it entirely, such that it becomes more personal. These generated images, together with a bit of JavaScript and the original PostGis database as a backup to the locations of points of interest are at the core of Google Maps.

Well, another interesting application of GIS information is by super-imposing data from different sources over the data in the database, or not rendering specific sets of data from the source in the database so that they have less information, making it easier to focus on the important bits. You can see how Bjørn Sandvik made a thematic mapper for Google Earth by generating KML from thematic data merged with (simplified versions of) world boundaries. Although KML takes some time to render, especially when in 3D (he wrote a nice, detailed paper about the techniques though), you can generate 2D images by loading your thematic data in PostGis first, then relating your data rows with the geographical data. Using a clever query and the pgsql2shp tool, it should be possible to output a file with the attributes you require for rendering. The last step is then to spit out an XML rendering file for mapnik, which basically filters your attributes, assigns colors or other styling measures and then run it through the mapnik renderer.

There's lots of things one can do here. Be reminded that dealing with these tools can be a bit daunting at first. There's generally no need to write complicated mergers/processors, because you can use PostGis as an intermediate data store, which can output .shp files (the most portable format I reckon), which other tools can visualize or process further.